[Baekjoon] 1647번 : 도시 분할 계획 (Python)

[Baekjoon] 1647번 : 도시 분할 계획 (Python)

 

목차

 

https://www.acmicpc.net/problem/1647

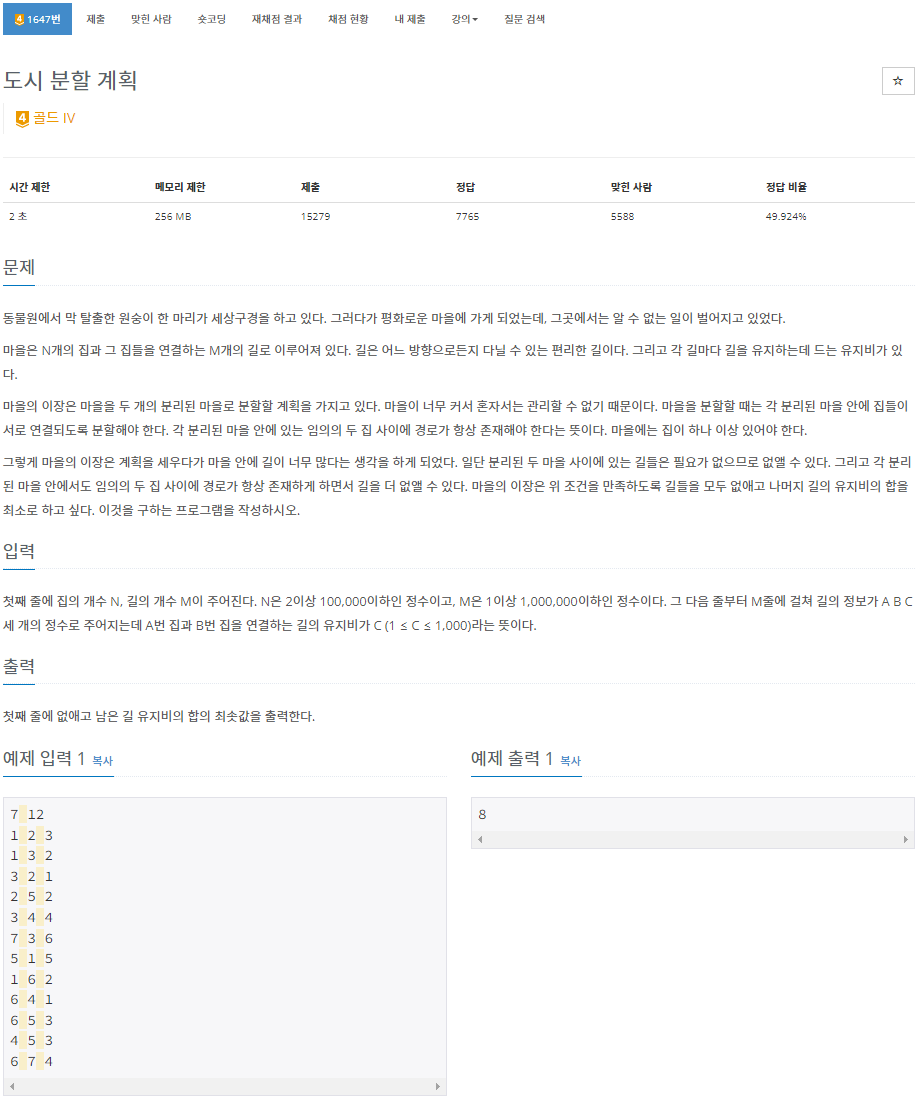
1647번: 도시 분할 계획

코드 링크

https://github.com/stellaluminary/Baekjoon

GitHub - stellaluminary/Baekjoon

Python

 

방법 1 - 메모리 198312KB / 시간 4048ms / 코드 길이 590B

 

본 문제는 그래프 이론. 최소 신장 트리를 활용한 Kruskal Algorithm이다.

 

본 문제를 풀기위해서는 서로소 집합 알고리즘과 이에 상응하는 사이클 제한 방법을 알아야한다.

 

최소 신장 트리를 위해서는 간선들에서 비용이 가장 낮은 순서대로 정렬을 한 후 차례로 한 집합으로 묶는 방법을 채택한다. 다만 이때 cycle이 없다는 사실을 알기위해 마지막 for문에 if f_p(p, a) != f_p(p, b):와 같은 조건문을 삽입한다.

 

또한, 마을을 2분할해야한다는 조건이 있는 본 문제의 특성상 사이클 없는 최소 신장 트리에서 마지막 간선만을 끊어주는 방식이 채택되어야 하기 때문에 last라는 value를 넣어 이를 해소한다.

 

유의 : sys.stdin.readline이 없으면 시간 초과가 발생함. 속도 차이

 

import sys
input = sys.stdin.readline

def f_p(p, x):
    if p[x] != x:
        p[x] = f_p(p, p[x])
    return p[x]

def union(p, a, b):
    a = f_p(p, a)
    b = f_p(p, b)
    if a < b:
        p[b] = a
    else:
        p[a] = b

n,m = map(int, input().split())

p = [0] * (n+1)
for i in range(n+1):
    p[i] = i

edges = []
for i in range(m):
    a, b, c = map(int, input().split())
    edges.append((c, a, b))

edges.sort()

res = 0
last = 0
for edge in edges:
    c, a, b = edge
    if f_p(p, a) != f_p(p, b):
        union(p, a, b)
        res += c
        last = c

print(res - last)

 

 

그림 이해 참조 : https://woongsin94.tistory.com/405

[백준 1647번] 도시 분할 계획(파이썬) / 크루스칼(MST)