Relativistic GAN Summary & Experiment (Relativistic discriminator: a key element missing from standard GAN)

1. 논문 정보

Jolicoeur-artineau, A. The relativistic discriminator: a key element missing from standard GAN. In ICLR, 2019.(2021.01.09 기준 citation 309)

arxiv.org/abs/1807.00734

The relativistic discriminator: a key element missing from standard GAN

In standard generative adversarial network (SGAN), the discriminator estimates the probability that the input data is real. The generator is trained to increase the probability that fake data is real. We argue that it should also simultaneously decrease th

arxiv.org

openreview.net/references/pdf?id=Bk1rZM6ZV

2. Relativistic discriminator 개괄

저자는 표준 GAN(SGAN)과는 다르게 실제 데이터가 진짜일 확률을 감소시켜야 한다고 주장한다.

이유

1) GAN 학습에 있어 미니 배치에서 데이터의 반이 fake image라는 사전 지식의 존재해야하기 때문

2) 발산(divergence) 최소화를 관측하기 위해서

3) SGAN이 IPM(integral probability metric) GAN과 매우 유사하다는 점

해당 목적을 위해 "relativistic discriminator"을 사용하면 됨을 보인다. 이 방법을 사용한 2가지 모델에 대해 보인다.

Relativistic GANs(RGANs)

해당 discriminator는 주어진 실제 데이터가 랜덤하게 뽑힌 가짜 데이터보다 더 현실적일 확률을 추정하는 것이다.

Relativistic average GANs(RaGANs)

해당 discriminator는 주어진 실제 데이터가 가짜 데이터들의 평균보다 더 현실적일 확률을 추정하는 것이다.

위 2개의 모델 방법론을 통해 나온 결과는 발산을 최소화하고 사전 지식을 가진채 설득력 있는 결과를 보인다. 이를 통해 적은 횟수의 반복으로 더 안정적이고 고해상도 이미지를 얻을 수 있다고 설명한다.

이와 관련한 결과를 먼저보면 다음과 같다.

보이는 바와 같이 일반적인 GAN은 학습에 있어 불안정하기 때문에 5천 번만큼의 반복을 진행하면 noise만 보이게 된다. 이에 반하여 Relativistic average discriminator를 SGAN(Standard GAN)에 적용한다면 많은 횟수임에도 불구하고 좋은 영상을 안정적으로 생성할 수 있음을 보이고 있다.

LSGAN 역시 마찬가지이다.

3. Relativistic Discriminator 동기

앞에서 이야기했던 것처럼 저자는 표준 GAN(SGAN)과는 다르게 실제 데이터가 실제일 확률을 감소시켜야 한다고 주장한다.

왜 그럴까?

이상적으로 SGAN은 Discriminator는 진짜 데이터든 가짜 데이터든 0.5에 평형점에 도달함을 이야기고 이를 수식 특히 Jensen-Shannon Divergence를 통해 증명했다.

$$min_G V(D^*, G) = 2 JSD(p_r||p_g) - 2log2$$

minimize D(x_r)=0.5, D(x_f)=0.5 일 때 JSD(P||Q)=0, $min_G V(D^*, G) = -2 log 2$

maximize D(x_r)=1, D(x_f)=0 일 때 JSD(P||Q)=log2, $min_G V(D^*, G) = 0$

해당 증명은 아래 링크를 참조하길 바란다.

jonathan-hui.medium.com/proof-gan-optimal-point-658116a236fb

Proof (GAN optimal point)

We have mentioned optimizing GAN is optimizing JS-divergence. This is not obvious from the cost function:

jonathan-hui.medium.com

그러나 위 그림에서 보이듯 Real data에 대한 discriminator의 성능은 1을 유지하고 있으며 생성된 이미지에 대한 discriminator 또한 0.5를 위해 가는 것이 아닌 1을 향한 성능을 보이고자 함을 확인할 수 있다. 이는 생성된 이미지와 실제 이미지 데이터가 각각 반씩 존재한다는 사실을 무시한 결과이다. 해서 relativistic discriminator를 통해 0.5에 갈 수 있도록 돕도록 gradient 정체가 없이 만드는 것이 해당 방법의 동기이다.

또 하나의 동기 해석은 gradient에 관한 것이다.

해당 gradient는 non-saturating SGAN에 서 discriminator와 generator의 gradient이다. 자세히 보면 지금 discriminator에서 약간의 차이가 확인이 가능한데 보통은 $D(x_r)$와 $(1-D(x_f))$ 순서로 적고 gradient 또한 그렇게 적는 것으로 알지만 위에서는 반대로 적혀 있다.

왜 그런지에 대해서는 알려주세요.... 저는 모르겠네요. ㅋ

아무튼 논문에서 설명하기를 discriminator가 optimal하다면 $D(x_r)=1$이고 이는 $(1-D(x_r))=0$을 의미한다. 이는 SGAN에서 discriminator의 gradient는 생성된 이미지에서 얻어진다는 것을 알 수 있다. 즉, 진짜 이미지로부터 사실적인 묘사를 학습시키는 것이 어렵다는 것을 의미한다.

이에 반하여 WGAN, WGAN-GP와 같은 IPM-based GAN은 위와 같은 gradient를 가지고 있으며 이를 통해 좋은 결과를 얻어낼 수 있다.

그러므로 SGAN이 IPM-based GAN과 같은 성질을 얻어내기 위해서 아래 3가지 요건이 필요하다.

1. SGAN의 discriminator step에서 $D(x_r)=0, D(x_f)=1$

2. SGAN의 generator step에서 $D(x_f)=0$

3. $C(x) \in F$

자세한 내용은 3.3 참조

번외

아래와 같은 해석이 가능하기도 하다.

참조 1. https://jonathan-hui.medium.com/gan-rsgan-ragan-a-new-generation-of-cost-function-84c5374d3c6e

Discriminator가 optimal하게 된다면 gradient가 사라지게 되는 정체구간이 생기게 된다. 이는 대부분의 초기 GAN이 겪는 문제들이며 이를 해결하기 위해 WGAN, WGAN-GP를 통해 clipping을 통한 Lipschiz constraint를 작동하게 하거나 gradient penalty를 통한 regularization로 gradient가 정체되지 않게 함으로써 나은 성능을 가지게 만들기도 합니다.

4. 방법

이 방법은 기존에 있는 다양한 GAN 종류에 대입시킴으로써 사용이 가능하다. 이를 통해 Relativistic GAN은 진짜 데이터가 생성된 이미지에 대해 얼마나 더 사실적인지를 나타내는 확률을 추정하는 방법을 시도한다.

RSGAN의 경우 아래와 같은 방식으로 수정을 진행한다. (왜 해당 내용으로 되는지에 대해서는 4 Method 4.1 Relativistic standard GAN 첫 부분을 확인하길 바란다.)

4.1 Relativistic Standard GAN(RSGAN)

해석 : random으로 sample된 가짜 데이터보다 주어진 진짜 데이터가 얼마나 더 사실적인가를 추정하는 확률을 discriminator가 확인

참고로 $L_D^{RSGAN}$에서 2개가 아니라 1개인 이유는 논문 참조.(간단)

4.2 Relativistic GANs(RGANs)

일반적인 GAN Loss를 (9), (10)을 통해 나타냅니다. 보통 GAN에서 C는 how realistic the input data is(입력 데이터가 얼마나 사실적인가)로 해석이 가능합니다.

해당 Loss를 (11), (12)와 같이 상대적인 평가로 수정하는 것이 바로 RGAN입니다. 이 때 generator loss도 위와 같이 변경된다는 점 잊지마세요. 이를 활용.하여 Standard GAN에 적용한 것이 바로 4.1에서 설명한 RSGAN입니다.

RGAN pseudocode

4.3 Relativistic average GANs(RaGANs)

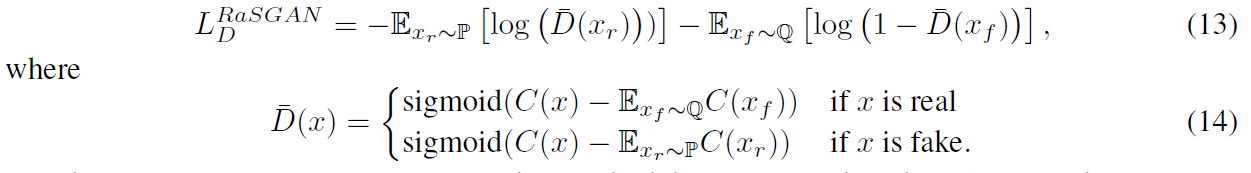
average를 붙인 것은 $L_D^{RaGAN}$에서 확인할 수 있듯 비교 대상이 앞에서는 random sample인 반면 여기서는 mini-batch의 expectation과 비교한다는 점이 차이가 있다.

TIP

개인적으로는 해당 방법이 조금 더 현실적이라는 점이라는 생각이 든다. 그 이유는 random sample로 뽑은 이미지가 화질이 나쁠 수도 있고 완전 realistic일 수도 있는데 그것이 모든 생성된 이미지를 대변하기에는 어려움을 겪을 수 밖에 없다고 생각하기 때문이다. 이런 점에서 개인적으로는 RaGAN 방식이 타당하다고 생각한다.

RaGAN pseudocode

5. 실험 결과

1) RGANs, RaGANs가 상당히 안정적이며 고품질 데이터 샘플을 생성함을 확인

2) gradient penalty를 가진 표준 RaGAN은 WGAN-GP에 비해 고품질 데이터를 생성함(SOTA를 위한 시간 400% 감소)

3) 작은 샘플에서 설득력 있는 고해상도 이미지(256x256) 생성이 가능함

spectral normalization을 가진 SGAN이나 WGAN-GP에 의해 생성된 것에 비해 더 향상된 고품질 이미지 생성됨.

5.1 CIFAR 10

Relativistic GAN을 사용하는 것이 낮은 FID를 얻을 수 있었다. 물론 RaHingeGAN와 RaSGAN-GP는 약간 예외

TIP

FID는 낮은 값이 좋은 결과를 의미합니다.

5.2 CAT

Appendix

해당 table은 저자가 애정을 가지고 만든 예시로 realistic한 결과가 어떻게 좋은 학습이 가능한지에 대해 보이고 있다.

1) 진짜 : 식빵(C=8), 가짜 : 개(C=-5)

SGAN : 식빵은 진짜다 : $P(x_r$ is bread)=1

RaGAN : 개에 비해 식빵은 realistic하다 : sigmoid(8-(-5)) = sigmoid(13)

2) 진짜 : 식빵(C=8), 가짜 : 개 엉덩이(식빵 같아 보이는 착각)(C=7)

SGAN : 식빵은 진짜다 : $P(x_r$ is bread)=1

RaGAN : 가짜 이미지는 진짜와 비슷하다. : sigmoid(8-7) = sigmoid(1)

3) 진짜 : 식빵(C=-3), 가짜 : 개(C=-5)

SGAN : 개처럼 보인다. 식빵이 아니다. : $P(x_r$ is bread)=0.05

RaGAN : 가짜와 진짜는 유사해보인다. : sigmoid(-3-(-5)) = sigmoid(2)

다른 GAN 모델에 Relativistic Discriminator 적용할 때의 Loss

아래 Official github에서 코드 확인 가능

github.com/AlexiaJM/RelativisticGAN

AlexiaJM/RelativisticGAN

Code for replication of the paper "The relativistic discriminator: a key element missing from standard GAN" - AlexiaJM/RelativisticGAN

github.com

개인적 시도

DCGAN에서의 relativistic discriminator 사용을 시도해보았습니다.

해당 내용 시도에 있어 celebA dataset을 사용했으며 21만장을 64x64로 줄여서 사용했고 이에 대한 결과는 다음과 같습니다.

test를 위한 fixed noise에 대한 0, 50, 100, 150, 200 epoch에 대한 결과와 train에서 사용한 latent vector에 대한 0, 50, 100, 150, 200 epoch에 대한 결과는 아래와 같습니다.

개인적 실험 : test를 위한 fixed noise에 대한 0, 50,100,150,200 epoch에 대한 결과

fixed latent vector : 0 epoch

fixed latent vector : 50 epoch

fixed latent vector : 100 epoch

fixed latent vector : 150 epoch

fixed latent vector : 200 epoch

개인적 실험 : 훈련에 사용한 gen_img 0, 50, 100, 150, 200 epoch 결과

train latent vector : 0 epoch

train latent vector : 50 epoch

train latent vector : 100 epoch

train latent vector : 150 epoch

train latent vector : 200 epoch

개인적 실험 결론

논문에서 제시한 결과를 더 관찰하기 위해서는 최소 5천번 일반적으로는 5만번의 epoch를 돌렸을 때 DCGAN과의 차이를 구해야 한다고 생각한다. 그러나 나는 사실 많은 epoch를 돌릴 수 있는 환경이 아니었기에 그런 실험을 하지 못했고 논문에서 보였듯 white noise가 생기는 혹은 GAN이 saturate되어 이미지의 결과가 좋지 못하게 나오는 것을 방지한다라는 결론을 나의 실험에서는 알기 어렵다.

그러나 위 실험을 진행하면서 느낀 점 중 하나는 relativistic discriminator 방법으로도 좋은 결과를 얻을 수 있을 것 같다는 생각이고 또 다른 하나는 해당 방법을 사용할 때 generator에 대해서도 loss를 상대적 비교를 해야한다는 점이 중요하다는 것을 알게되었다.

실험을 위해 Generator의 loss에 있어 일반적 GAN이 사용하는 방법 혹은 relativistic discriminator gan의 한 부분만을 사용하는 방법(fake 결과와 real data 평균값을 뺀 값만을 loss에 넣어 사용하는 방법 : 아래 Generator Loss의 왼쪽 부분만 사용)을 해보았더니 10 epoch 동안에 일반적인 방법에 비해 특징을 잡는데 어려움을 겪었다.