PR-119 "Active Learning For Convolutional Neural Networks: A Core-Set Approach" Review (2018 ICLR)()

PR-119 "Active Learning For Convolutional Neural Networks: A Core-Set Approach" Review (2018 ICLR)()

 

 

목차

 

 

 

 

1. Citations & Abstract 읽기

Citations : 2022.01.04 기준 581회

저자

Ozan Sener - Intel Labs

Silvio Savarese - Stanford University

Abstract

 

CNN은 범용 레시피를 사용하여 많은 인식 및 학습 작업에 성공적으로 적용되었다. 지도 예제의 매우 큰 데이터 세트에서 깊은 모델을 훈련시킴. 그러나 label 지정된 큰 이미지를 모으는 것이 비용이 많이 들기 때문에 이 접근 방법은 현실에서는 다소 제한적이다. 이 문제를 완화하는 한 가지 방법은 active learning과 같은 매우 큰 수집들로부터 label이 되어진 이미지들을 선택하는 영리한 방법들을 제안하는 것이다.

우리들의 경험적 연구는 문헌에서 많은 active learning heuristics이 배치 환경에서 CNN을 적용할 때 효과적이지 않다는 것을 제안한다. 이러한 제한점들에서 영감을 받아, 우리는 core-set selection으로써의 active learning 문제를 정의한다. 즉, 선택된 하위 집합에 대해 학습된 모델이 남아있는 데이터 포인트들에 대해 경쟁력이 있도록 포인트 세트를 선택하는 것. 또한, 우리는 데이터 포인트의 기하학적 구조를 사용함으로써 어떤 선택된 하위집합의 성능을 특징화하는 이론적인 결론을 제시한다. active learning algorithm으로써 우리는 우리들의 특성화에 따라 가장 좋은 결과를 산출할 것으로 예상하는 하위집합을 선택한다. 우리들의 실험은 제안된 방법이 큰 margin에 의한 이미지 분류 실험에서 현존하는 접근법들보다 상당히 크게 능가함을 보여준다.

 

 

 

제한점을 개선하기 위한 새로운 Active Learning 문제를 정의함.

특성화에 잘 고려된 하위집합을 선택하여 큰 성과가 보임을 증명.

 

2. 발표 정리

https://youtu.be/3ROQis3hxPs

 

 

공식 논문 링크

https://openreview.net/forum?id=H1aIuk-RW 

Active Learning for Convolutional Neural Networks: A Core-Set Approach

https://arxiv.org/abs/1708.00489

Active Learning for Convolutional Neural Networks: A Core-Set Approach

Presentation Slide

None

Contents

 

Active Learning이란

Label을 지정할 때 어떤 것을 먼저 지정해야할 것인가

(첨언 : Active Learning은 데이터에 라벨을 붙일 때 성능이 높게 나올 수 있도록 데이터를 선별함으로써 딥러닝 모델의 효율성을 높이는 학습법이다.)

 

실제로 현업에서 Labeling을 계속 하는 중

 

실험 결과

 

빨간색은 Random으로 label 매긴 것

분홍색은 제안된 방법

분홍색이 가장 좋은 Accuracy를 나타냄을 확인할 수 있음

데이터가 많은 곳에서 효율적으로 Label을 하기 위한 곳에서 Active Learning의 효과가 발현될 가능성이 높다고 판단

 

Summary

- Active Learning as a Core-Set Selection Problem (Core-Set Selection 문제로 놓고 능동학습을 진행)

- Using discrete optimization based methods (이산 최적화를 활용)

- Significantly outperforms existing approaches (현존 방법들 대비 능가하는 성능)

 

Introduction

- These practical considerations raise a critical question: “what is the optimal way to choose data points to label such that the highest accuracy can be obtained given a fixed labeling budget.”

- The goal of active learning is to find effective ways to choose data points to label, from a pool of unlabeled data points, in order to maximize the accuracy.

active learning의 목표는 효과적인 label할 데이터를 뽑아 label하는 것

- We experiment with many of these heuristics in this paper and find them not effective when applied to CNNs.
CNN 모델에 효과적이지 않음

- In the classical setting, the active learning algorithms typically choose a single point at each iteration; however, this is not feasible for CNNs

- In order to tailor an active learning method for the batch sampling case, we decided to define the active learning as core-set selection problem.

active learning을 core-set selection problem이라 정의

 

tailor (특정한 목적·사람 등에) 맞추다[조정하다]

 

Related Work

Uncertainty Quantification

- $argmin P(y_1|x)$

- $argmin P(y_1|x) - P(y_2|x)$

- Entropy

Some Active Learning Methods

- Uncertainty Sampling

- Query By Committee (QBC) : Ensemble

- Expected Model Change

- Expected Error Reduction

- Variance Reduction

- Density Weighted Methods

 

MIDAS

 

Active Learning

 - Bayesian active learning methods

- Uncertainty based methods

- Optimization based methods

- Discrete optimization based method

 

Core-Set Selection

- Define active learning as a core-set selection problem

- try to choose a subset of it such that the model trained on the selected subset will perform as closely as possible to the model trained on the entire dataset

subset을 활용하여 훈련시키는 것이 전체 데이터 세트를 훈련시키는 것만큼의 효과를 내는 것

 

Weakly-Supervised Deep Learning

- we experiment the active learning both in the fully-supervised and weakly-supervised scheme.

- Using Ladder networks

 

Ladder networks

supervised & unsupervised 합쳐서 동시에 학습 진행이 가능하게 함. 이하 생략.

 

Problem Definition

Compact Space $\mathcal{X}$

Label Space $\mathcal{Y}={1,...., C}$

Loss Function $l(\cdot ,\cdot ; w) : \mathcal{X} \times \mathcal{Y} \rightarrow \mathcal{R}$

 

 

초기 Uniform Random으로 data-point를 뽑음

n : x 전체 샘플 수

m : n 중 label을 알고 있는 것

 

 

 

 최소화하고 싶은 loss Expectation값을 다음과 같이 나타낼 수 있음.

 

Generalization Error

- theoretically to be bounded

- typically generalize well for various visual problems

 

Training Error

- very low training error

 

Core-Set Loss

- critical part for active learning

 

(CNN의 뛰어난 성능 때문에 Generalization Error와 Training Error 0으로 가정)

 

Re-define the active learning problem

 

Subset에서의 모델 성능과 전체 데이터 세트의 성능 차이 최소화 

 

 Bound 증명 Theorem 1

 

 

n : 전체 sample

s : core-set

 

$\delta_s$가 얼마나 되야 조건식을 만족시킬 수 있을지 모름.

고로 계속 Update Interation으로 간격을 줄이고 Lower Bound와 Upper Bound가 같을 때 Optimal Solution이라 판단.

 

Solving the K-Center Problem 

 

 

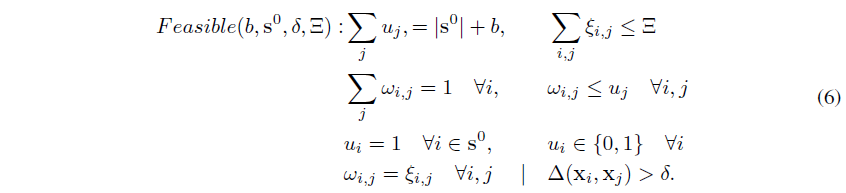
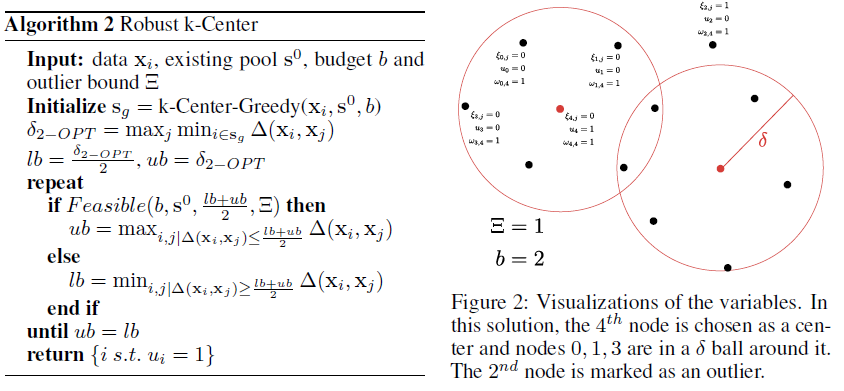
VGG16 사용

RMSProp

Tensorflow

Tool : Gurobi

 

 

CIFAR, SVHN 이미지 데이터 세트

다른 방법들과 비교

 

 

 

Table 1 Distance Matrix 만드는데 측정 시간이 오래걸림

Fig 6 Greedy만 써도 다른 어떤 방법보다 좋음

 

 

 

 

참조

GitHub

 

블로그

https://kmhana.tistory.com/6

Active Learning을 위한 딥러닝 - Core-set

 

https://blog.lgcns.com/2275

족집게 데이터가 '전교 1등' AI 만든다!

 

https://www.youtube.com/watch?v=Gio7MU5nnc4