Gram matrix (그람 행렬) 정리
Gram matrix (그람 행렬) 정리
시작에 앞서
만약 Gram matrix를 찾아본다면 아마도 2016 CVPR L. A. Gatys et al. 연구진들이 제안한 Style Transfer에 나와있는 style loss 구성의 일부를 확인하셨기 때문으로 판단됩니다.
만약 해당 논문 정리를 살펴보기 원하신다면 아래 링크를 확인해주세요.
https://aigong.tistory.com/359
[논문 Summary] Neural Style Transfer (2016 CVPR) "Image Style Transfer Using Convolutional Neural Networks"
[논문 Summary] Neural Style Transfer (2016 CVPR) "Image Style Transfer Using Convolutional Neural Networks" 목차 논문 정보 Citation : 2022.02.10 목요일 기준 3527회 저자 Leon A. Gatys / Alexander S...
aigong.tistory.com
Style Transfer에서의 Gram matrix 설명
논문에서 사용하는 feature map의 size는 pytorch 기준으로 다음과 같이 나타냅니다.
feature map $F \in R^{N_l \times M_l}$
이때의 $M_l$은 모든 픽셀의 수, 다른 말로 표현하면 height와 width의 곱입니다.
feature map이 batch size, channel, height, width라면 F는 (channel, height *width)라고 표현이 가능한 것입니다.
cf) style transfer에서의 batch size=1
이를 도식화하면 다음과 같이 표현할 수 있습니다.
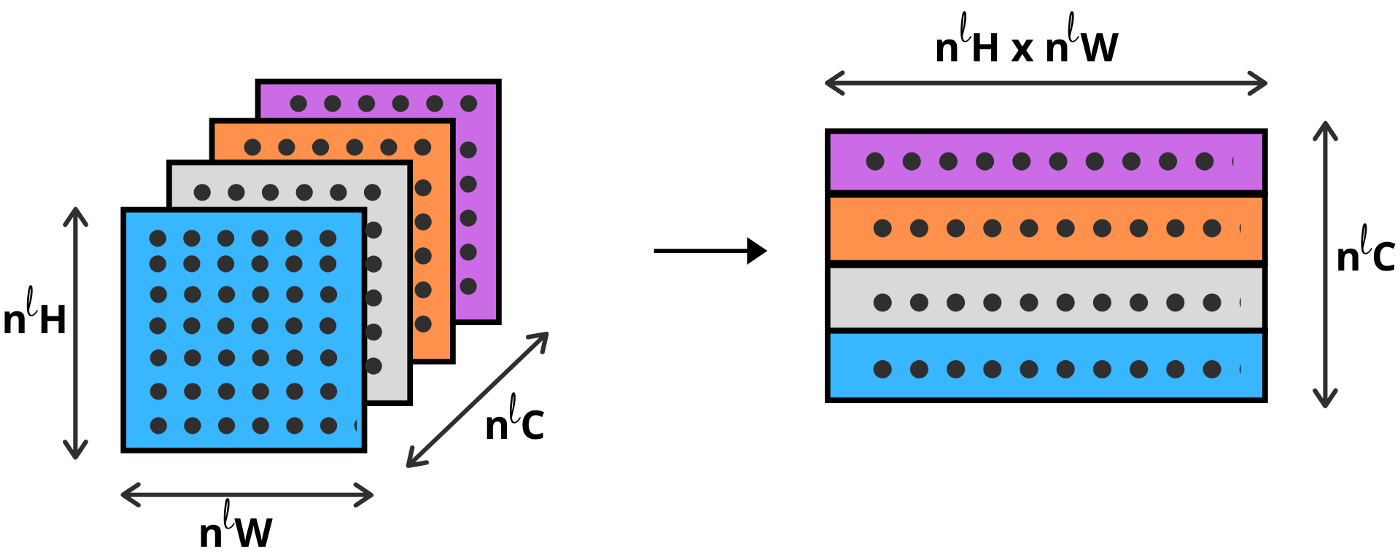
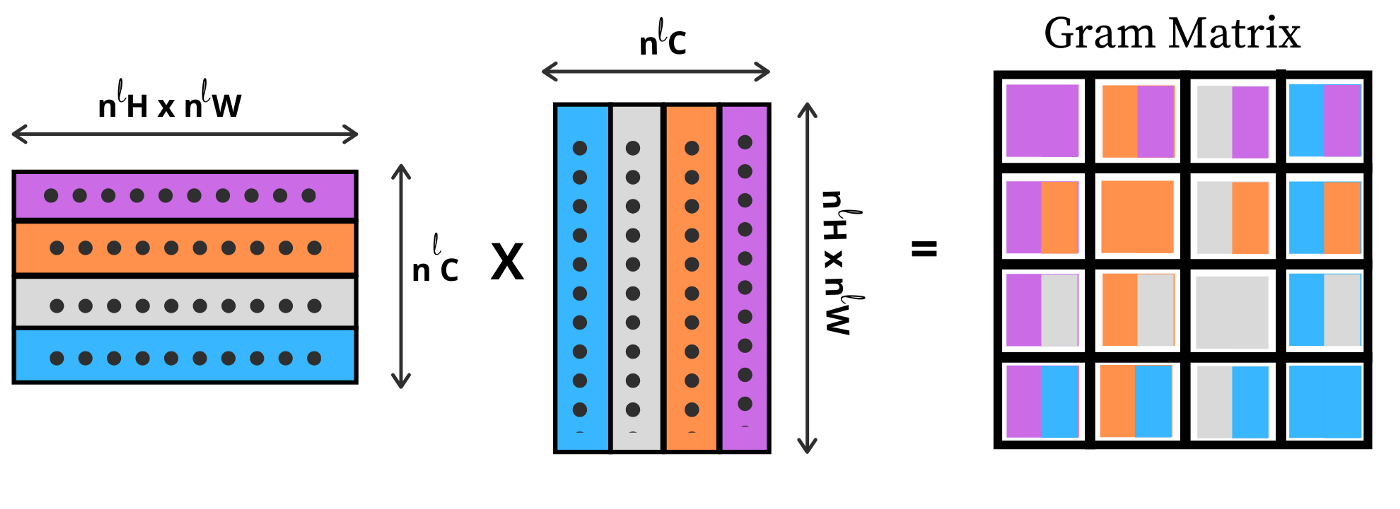
Gram matrix는 vector들의 집합인 $v_1, ... , v_n$들의 내적을 진행하는 것으로 $G_{i,j} = <v_i, v_j>$와 같이 표기 가능합니다. 즉, 위에서 우리가 만든 2차원의 feature map을 아래와 같이 matrix multiplication을 통해 gram matrix를 구성할 수 있습니다.
다시 말해 $v_1, ... , v_n$로 구성된 V라는 matrix를 행렬곱을 하면 G를 얻는다는 것입니다.
$$G=V^T V$$
일반화된 Gram matrix 설명
조금 이해하기 쉽게 홍정모 연구소 YouTube 채널의 설명 (Reference 2)를 참조하여 설명해보겠습니다.
만약 1개의 filter 내 2차원의 이미지가 존재한다고 한다면 $[1, h, w]$와 같이 표기가 가능합니다.
이를 vectorize하기 위해 h와 w를 곱한 값으로 표기하겠습니다.
$$[1, h \times w]$$
이를 자세히 들여다보면 한 개의 필터에 대한 한 행의 벡터로 구성됨을 알 수 있습니다.
이때 $h \times w=3$이고 1x3의 형태를 가지는 vector $\vec{x}$가 존재한다고 가정해보겠습니다. 표기는 다음과 같게 표현할 수 있습니다.
$$\vec{x}=[x_0, x_1, x_2]$$
만약 filter가 2개라면 다음과 같이 표기 가능합니다.
$$\begin{vmatrix} \vec{x_1} \\ \vec{x_2} \end{vmatrix} = \begin{vmatrix} x_0^1 & x_1^1 & x_2^1 \\ x_0^2 & x_1^2 & x_2^2 \end{vmatrix}$$
YouTube에서 설명하는 표기로 바꿔 설명하면 다음과 같습니다.
필터 표기는 $F=N=2$이고, pixel의 수인 $M=3$.
$$\mathbf{F} = \begin{vmatrix} Z_0(x_0) & Z_0(x_1) & Z_0(x_2) \\ Z_1(x_0) & Z_1(x_1) & Z_1(x_2) \end{vmatrix} = \begin{vmatrix} F_{00} & F_{01} & F_{02} \\ F_{10} & F_{11} & F_{12} \end{vmatrix}$$
$$F_{ik} = Z_i (x_k)$$
$F_{ik}$는 $Z_i$ 필터에 $x_k$ 픽셀을 넣었을 때의 value를 의미합니다.
여기서 Gram matrix $G$를 구하기 위해 위에서 배운 행렬 곱을 진행하면 다음과 같습니다.

$$G_{i,j}= \sum_k F_{ik} F_{jk}=\begin{vmatrix} F_{00}F_{00} + F_{01}F_{01} + F_{02}F_{02} & F_{00}F_{10} + F_{01}F_{11} + F_{02}F_{12} \\ F_{10}F_{00} + F_{11}F_{01} + F_{12}F_{02} & F_{10}F_{10} + F_{11}F_{11} + F_{12}F_{12} \end{vmatrix}$$
$$\sum_k \begin{vmatrix} F_{0k}^2 & F_{0k}F_{1k} \\ F_{1k}F_{0k} & F_{1k}^2\end{vmatrix}$$
이 행렬의 모습은 covariance matrix (공분산 행렬)과 매우 닮아 있습니다.
$$C[X, Y] = \begin{vmatrix} Var[X] & Cov[X, Y] \\ Cov[Y, X] & Var[Y] \end{vmatrix}$$
$$Cov(X,X)=Var(X), Cov(X,Y)=Cov(Y,X)$$
이를 간략하게 풀어설명하면 분포를 맞춘다고 보면 됩니다.
Gram matrix에 대한 이해
논문에서 얻게 되는 Gram matrix $G^l \in R^{N_l \times N_l}$의 형태를 가집니다.
조금 이해하기 쉽게 변형하면 channel을 의미하는 c로 변형해서 설명할 수 있습니다.
$$G^l \in R^{c_l \times c_l}$$
그렇다면 이 행렬을 어떤 식으로 이해하면 될까요?
아마 Gram matrix의 결과는 특정 layer l에 대하여 feature map의 channel 간 correlation 정보를 담아 중요한 상관관계의 값을 찾는 것입니다.
제 개인적인 생각은 차원 축소를 진행하고 특정 layer l에서의 correlation을 찾아 그 정보를 비슷하게 함으로써 texutre에 대한 정보를 뽑을 수 있었던 것이 아니었나 하는 생각이 들었습니다.
고로 우리가 style transfer에서 gram matrix 간 오차를 줄이게 함으로써 서로의 분포 차이를 줄이고 상관관계를 높여 유사한 style을 찾도록 유도하는 것으로 해석할 수 있을 것 같습니다.
Reference
1. Wiki - Gram matrix (eng & kor)
https://en.wikipedia.org/wiki/Gram_matrix
Gram matrix - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Matrix of inner products of a set of vectors In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors v 1 , … , v n {\displaystyle v_{1},\dots ,v_{n}} in a
en.wikipedia.org
https://ko.wikipedia.org/wiki/%EA%B7%B8%EB%9E%8C_%ED%96%89%EB%A0%AC
그람 행렬 - 위키백과, 우리 모두의 백과사전
다음은 그람 행렬에 관한 설명이다. 실수체에서 정의하는경우 , 그람 매트릭스(그람 행렬) G는 어떤 벡터 M 과 그들의 집합 V를 예약했을때, 이들의 내적 곱의 모든 경우의 행렬 표현이다. 즉, G(ij)
ko.wikipedia.org
2. YouTube - 홍정모 연구소 - Gram Matrix 설명 (Style transfer)
3. ML Wiki -
http://mlwiki.org/index.php/Gram_Matrices
Gram Matrices - ML Wiki
Gram Matrices A Gram matrix of vectors $\mathbf a_1 , \ ... \ , \mathbf a_n$ is a matrix $G$ s.t. $G = \langle \mathbf a_i, \mathbf a_j \rangle$ for all $i,j$ if vectors $\mathbf a_1 , \ ... \ , \mathbf a_n$ are columns of a matrix $A$, then $G = A^T A$ a
mlwiki.org
4. 공분산 Covariance
https://ko.wikipedia.org/wiki/%EA%B3%B5%EB%B6%84%EC%82%B0
공분산 - 위키백과, 우리 모두의 백과사전
두 개의 확률 변수 X 와 Y 의 상관성과 공분산의 부호. 공분산(共分散, 영어: covariance)은 2개의 확률변수의 선형 관계를 나타내는 값이다.[1] 만약 2개의 변수중 하나의 값이 상승하는 경향을 보일
ko.wikipedia.org






